Minimax Algorithm for Game AI: Alpha-Beta Pruning, Cutoff Search, Expectimax

Introduction

The quest to create intelligent game-playing agents has captivated researchers for decades. Particularly, two-player games like chess have served as a proving ground for AI algorithms. Today, we'll explore the foundational Minimax algorithm and its powerful enhancements, including alpha-beta pruning, cutoff search, and expectimax.

The Minimax Algorithm: A Historical Perspective

The concept of Minimax was first proposed by Claude Shannon in his seminal 1959 paper, "Programming a Computer for Playing Chess." This algorithm laid the groundwork for game AI. Its significance was further cemented in 1997 when IBM's Deep Blue, powered by Minimax, defeated chess world champion Garry Kasparov. This moment was a turning point, proving that AI could outperform human intelligence in strategic decision-making.

Understanding the Core Principles

At its core, the Minimax algorithm is a tree-based search method that enables an AI agent to make optimal moves by considering all possible future game states. It follows a depth-first search (DFS) approach, where the game is represented as a tree of possible moves, and the algorithm explores each branch to evaluate the best possible action.

However, one of the biggest challenges in game-playing AI is the size of the state space. For instance, chess has an enormous number of possible board configurations, and Go, another complex game, has an estimated $10^170$ possible board positions. Searching through all possible states is computationally infeasible, making it necessary to enhance the basic Minimax algorithm with more efficient techniques.

Minimax is a depth-first search algorithm designed to find the optimal move in a two-player, zero-sum game. A zero-sum game implies that one player's gain is the other's loss. We designate the two players as "Max" (our agent) and "Min" (the opponent).

Key Characteristics of the Environment:

• Fully Observable: All game states are visible to both players.
• Discrete: Actions and states are finite and distinct.
• Deterministic: No element of chance is involved.
• Adversarial: An opponent exists, requiring strategic planning.
• Limited Time: Decisions must be made within a reasonable timeframe.

Formalizing the Game:

To implement Minimax, we define the game using these components:

• Initial State: The starting configuration of the game.
• Move Function: Determines whose turn it is at any given state.
• Actions Function: Lists all possible actions at a state.
• Result Function: Defines the resulting state after an action is performed.
• Terminal Test: Checks if the game has reached a terminal (end) state.
• Utility Function: Assigns a numerical value to each terminal state, indicating the outcome.

Minimax Game Tree

Minimax constructs a game tree, where nodes represent game states and edges represent actions. The algorithm assigns a minimax value to each node, representing the best achievable outcome for a player at that state.

• Max aims to maximize the utility value.
• Min aims to minimize the utility value.

An example game tree for tic-tac-toe is shown below. We begin with an empty $3×3$ grid, where the Max player (playing as 'X') makes the first move. Max can place 'X' in any of the nine available positions. Once Max plays, it becomes Min’s turn (playing as 'O'), who can now place 'O' in any of the remaining eight positions. The game alternates between Max and Min until reaching a terminal state (a win, loss, or draw).

At the terminal nodes of the game tree, we evaluate the outcomes using a utility function:

• If Max wins, the state is assigned a utility value of +1.
• If Min wins, the state is assigned a utility value of −1.
• If the game ends in a draw, the state is assigned a utility value of 0.

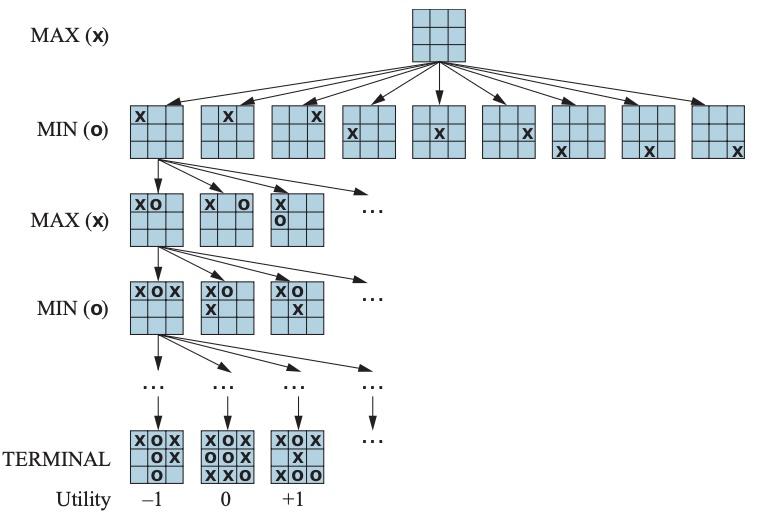
How Minimax Works

To better grasp the mechanics of Minimax, let's analyze a simplified game scenario. Instead of tackling Tic-Tac-Toe, we'll consider a trivial game with a manageable state space, allowing us to visualize the entire process on a single diagram.

In this game, the Max player has three initial actions: a1, a2, and a3. If Max chooses a1, the game transitions to state B, where the Min player then has three possible actions: b1, b2, and b3. Each of these Min actions leads to a terminal state with a defined utility value. Similarly, actions a2 and a3 lead to their respective sets of Min actions and terminal states.

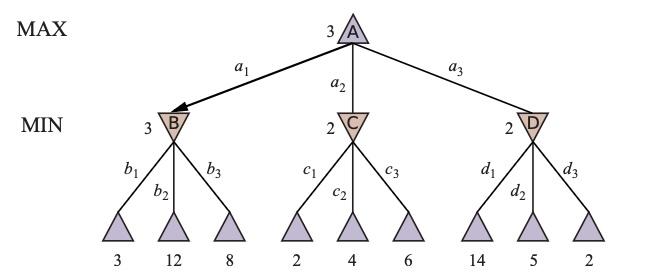
This game is "one move deep," meaning each player makes a single move before reaching a terminal state. We assign utility values to each terminal state, reflecting the outcome for the Max player. For instance, a value of 14 indicates a win for Max, while a value of 2 signifies a win for Min.

Imagine we are at the root node and Max must choose between a1, a2, and a3. A naive approach might be to select a3, aiming for the highest utility of 14. However, this ignores the Min player's strategy. Min would inevitably choose the action that minimizes Max's utility, leading to a potentially unfavorable outcome.

To make an informed decision, we must anticipate the Min player's moves. If Max chooses a1, Min would select a1, resulting in a utility of 3. If Max chooses a3, Min would select a2, resulting in a utility of 2. If Max chooses a2, Min would select c1, resulting in a utility of 2. Therefore, the optimal move for Max is a1, guaranteeing a utility of 3, which is better than the alternative outcomes.

The Minimax Value

The Minimax algorithm formalizes this reasoning by assigning a Minimax value to each node, representing the best achievable utility for the player at that node. We calculate these values recursively, starting from the terminal nodes and working our way up to the root.

To determine the Minimax value of the root node (A), we first need the Minimax values of its children (B, C, and D). Since B, C, and D are Min nodes, their Minimax values are the minimum of their respective children's utility values. For instance, the Minimax value of B is 3 (the minimum of 3, 12, and 8).

Once we have the Minimax values of B, C, and D, we can calculate the Minimax value of A. As A is a Max node, its Minimax value is the maximum of its children's Minimax values, which is 3.

Recursive Computation

The Minimax algorithm employs a recursive depth-first search to traverse the game tree. At each terminal node (base case), the utility value is directly returned. At non-terminal nodes, the algorithm recursively calls itself on the child nodes, selecting the maximum or minimum value based on whether it's a Max or Min node. The pseudocode for the Minimax algorithm is as follows:

def minimax(node, depth, maximizingPlayer):
    if depth == 0 or node is a terminal node:
        return the heuristic value of node
    if maximizingPlayer:
        value = -∞
        for child in node.children:
            value = max(value, minimax(child, depth - 1, False))
        return value
    else:
        value = +∞
        for child in node.children:
            value = min(value, minimax(child, depth - 1, True))
        return value

Depth-First Traversal and Node Evaluation Order

Lets apply the algorithm to the game tree shown below. The Minimax algorithm essentially performs a depth-first search (DFS). In our example, the nodes are assigned the minimax value in the following order: K, L, E, M, N, F, B, O, G, P, Q, H, C, R, I, S, T, J, D, A. This sequence reflects the recursive calls made during the DFS traversal.

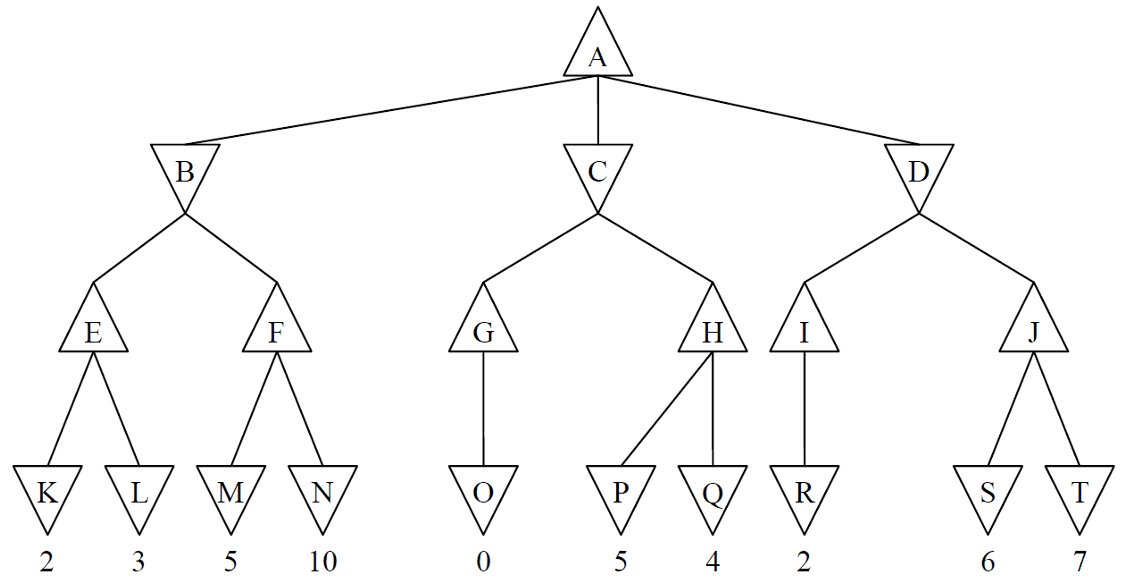
Properties of Minimax Search

Minimax search is both complete (guaranteeing a solution if the state space is finite) and optimal (finding the best possible move). However, its time complexity is $O(b^m)$, where $b$ is the branching factor and $m$ is the depth of the game tree. In chess, for example, $b$ is approximately 35, and $m$ can reach around 100 in a reasonable game, leading to an enormous state space. This exponential complexity makes optimizations like alpha-beta pruning essential for handling complex games efficiently.

Enhancing Minimax: Alpha-Beta Pruning

While Minimax guarantees optimal moves, its time complexity can be prohibitive for complex games. Alpha-beta pruning offers a significant improvement by reducing the search space without sacrificing optimality.

The fundamental question we address is: can we make the correct decision without examining every state in the game tree? Alpha-beta pruning achieves this by intelligently pruning branches that cannot influence the final outcome. It does that by keeping track of two values at each node:

• Alpha ($\alpha$)): Represents the best (highest) value found so far for the Max player.
• Beta ($\beta$): Represents the best (lowest) value found so far for the Min player.

The Process:

1. Initialization: At the root node, $\alpha$ is initialized to negative infinity and $\beta$ to positive infinity.
2. Value Propagation: $\alpha$ and $\beta$ values are passed down the game tree during recursive calls.
3. Pruning Conditions:
   • Max Nodes: If a node's temporary value $v$ is greater than or equal to $\beta$, prune the remaining branches.
   • Min Nodes: If a node's value $v$ is less than or equal to $\alpha$, prune the remaining branches.
4. Value Updates:
   • Max nodes update $\alpha$ to the highest value encountered.
   • Min nodes update $\beta$ to the lowest value encountered.
5. Ordering Matters: The order in which nodes are visited significantly impacts pruning effectiveness. Optimal ordering maximizes pruning.

The algorith to is given below:

def alpha_beta(node, depth, alpha, beta, maximizingPlayer):
    if depth == 0 or node is a terminal node:
        return the heuristic value of node
    if maximizingPlayer:
        value = -∞
        for child in node.children:
            value = max(value, alpha_beta(child, depth - 1, alpha, beta, False))
            alpha = max(alpha, value)
            if alpha >= beta:
                break
        return value
    else:
        value = +∞
        for child in node.children:
            value = min(value, alpha_beta(child, depth - 1, alpha, beta, True))
            beta = min(beta, value)
            if beta <= alpha:
                break
        return value

Example

This video provides a visual walkthrough of alpha-beta pruning. It illustrates how the algorithm efficiently explores a game tree using depth-first search, while eliminating unnecessary branches. As the tree is traversed, you'll see the temporary minimax values ($v$) calculated for each node. These values are then compared against the dynamically updated alpha and beta bounds, which are inherited from parent nodes during recursive calls. This comparison determines when pruning occurs, significantly reducing the search effort.

Cutt off Search

In practice, game trees can be vast, making it impossible to search all the way to the terminal states. Alpha-beta pruning improves Minimax, but even it struggles with the sheer size of game trees. In many real-world scenarios, searching all the way to terminal states simply isn't practical. This is where cutoff search becomes indispensable.

Cutoff search addresses this challenge by limiting the depth of our exploration. Instead of reaching the end of every branch, we define a cutoff point where the search stops. At this point, we use an evaluation function to estimate the utility of the current state, replacing the traditional utility function used at terminal states. We also replace the terminal test with a cutoff test to know when to stop searching.

The depth of the search directly correlates with the agent's skill. A 4-ply lookahead in chess results in a player with limited abilities, comparable to a human novice. On the other hand, an 8-ply search approximates the skill level of a typical PC or a human master. Deep Blue, the legendary chess-playing AI, was known to explore certain lines of play up to an impressive 40 plies deep.

Expectimax: Dealing with Uncertainty

Minimax and its enhancements assume the opponent is playing optimally. However if the opponent is not rational or the game involves an element of chance, we need a different approach. Expectimax is an extension of Minimax designed for games with uncertainty, such as card games or board games with dice. It accounts for the probabilistic nature of these games by considering all possible outcomes weighted by their probabilities. The algorithm assign expected value for the Min nodes, which is the average of the possible outcomes. For the max nodes, it selects the action that maximizes the expected value.

Conclusion

In this blog, we've journeyed through the core of game-playing AI, starting with the foundational Minimax algorithm. We've seen how Minimax, with its depth-first search strategy, provides a framework for optimal decision-making in two-player, zero-sum games. However, we also acknowledged its limitations in handling the vast state spaces of complex games.

To address these limitations, we delved into powerful enhancements like alpha-beta pruning, which significantly reduces the search space without compromising optimality. We further examined cutoff search, a practical approach to managing computationally intensive games by limiting search depth and employing evaluation functions. Finally, we touched upon Expectimax, highlighting its role in handling games with uncertainty and probabilistic outcomes.

Frequently Asked Questions (FAQs)

1. What is the Minimax algorithm?

The Minimax algorithm is a decision-making algorithm used in two-player, zero-sum games. It recursively explores the game tree, assigning minimax values to nodes, to determine the optimal move for the maximizing player (Max), assuming the minimizing player (Min) plays optimally.

2. What is a zero-sum game?

A zero-sum game is a situation in which one player's gain is equivalent to another player's loss, so the net change in wealth or benefit is zero.

3. What is alpha-beta pruning?

Alpha-beta pruning is an optimization technique for the Minimax algorithm that reduces the search space by eliminating branches of the game tree that cannot affect the final decision. It uses alpha and beta values to track the best possible outcomes for Max and Min players, respectively.

4. How does alpha-beta pruning improve Minimax?

Alpha-beta pruning improves Minimax by reducing the number of nodes that need to be evaluated in the game tree. This results in faster computation and allows for deeper searches within time constraints, without sacrificing optimality.

5. What are alpha and beta values in alpha-beta pruning?

• Alpha (α): The best (highest) value found so far for the Max player.
• Beta (β): The best (lowest) value found so far for the Min player.

6. What is cutoff search?

Cutoff search is a technique used when it's impractical to search the entire game tree to terminal states. It limits the search depth and uses an evaluation function to estimate the utility of non-terminal states.

7. Why is cutoff search necessary?

Cutoff search is necessary because many real-world games have vast state spaces that make it computationally impossible to search all the way to terminal states. It allows for a balance between accuracy and time efficiency.

8. What is an evaluation function?

An evaluation function is a heuristic function that estimates the utility of a non-terminal state in a game. It provides an approximation of the state's value, allowing the algorithm to make decisions without reaching terminal states.

9. What is Expectimax?

Expectimax is an extension of the Minimax algorithm designed for games with chance elements or uncertainty. It calculates the expected value of possible outcomes, weighted by their probabilities.

10. When should Expectimax be used instead of Minimax?

Expectimax should be used when the game involves chance elements (like dice rolls or card draws) or when the opponent's moves are not guaranteed to be optimal.

11. Does alpha-beta pruning always find the optimal move?

Yes, alpha-beta pruning guarantees the same optimal move as the Minimax algorithm. It only reduces the search space, not the quality of the decision.

12. How does the order of node evaluation affect alpha-beta pruning?

The order of node evaluation significantly impacts the effectiveness of alpha-beta pruning. Optimal ordering maximizes pruning, while poor ordering may result in minimal or no pruning.

13. What is the time complexity of the Minimax algorithm?

The time complexity of the Minimax algorithm is $O(b^m)$, where b is the branching factor (number of possible moves at each state) and m is the depth of the game tree.

14. How does cutoff search affect the accuracy of the game-playing agent?

Cutoff search trades perfect accuracy for faster results. By limiting the search depth, the agent may not find the absolute optimal move, but it can make reasonably good decisions within time constraints.

15. Can these algorithms be used for games with more than two players?

While Minimax is designed for two-player games, variations and extensions of these algorithms can be adapted for games with more than two players, although the complexity increases significantly.