BFS, DFS, Uniform Cost Search and A* Algorithms: Mastering Search Techniques in AI Problem Solving

Introduction

Problem-solving in AI is a fascinating field that focuses on finding efficient solutions to complex challenges. One classic example is the navigation problem, where an AI system must determine the optimal route from one point to another. The state space represents all possible situations or configurations that can occur in a problem. In our navigation example, each state might represent a different location or intersection. AI problem-solving often involves an offline simulated exploration of this state space, where the system examines various possibilities without actually moving in the real world.

This exploration is where search algorithms come into play. These algorithms systematically traverse the state space, evaluating different paths and outcomes to find the best solution. However, before we can apply these algorithms, we need to formulate the problem correctly.

Problem Formulation

Problem formulation is crucial in AI problem-solving and consists of five key elements:

1. Initial State: This is the starting point of our problem. In a navigation scenario, it would be the current location. For example, in a maze-solving problem, it might be the entrance of the maze.

2. Actions: These are the possible moves or decisions that can be made from any given state. For navigation, actions might include "turn left," "go straight," or "turn right" at each intersection. In a puzzle-solving context, actions could be moving tiles in a sliding puzzle. The implementation typically includes a function actions(state) that returns a list of possible actions from a given state.

3. Transition Model: This defines how each action changes the current state. It specifies what new state results from applying a particular action to the current state. For instance, in a chess game, it would determine the new board configuration after a move. The implementation usually involves a function transition(state, action) that returns the new state after applying the action to the current state.

4. Goal Test: This is a way to determine whether a given state is the goal state we're aiming for. In navigation, it would check if we've reached our destination. In a puzzle-solving scenario, it might check if the current configuration matches the solved state. The implementation typically includes a function goal_test(state) that returns True if the state is the goal state, False otherwise.

5. Path Cost: This assigns a numeric cost to each path through the state space. It helps in evaluating the efficiency of different solutions, such as finding the shortest or fastest route. In a navigation problem, it might represent distance or time. The implementation usually involves a function path_cost(state, action, next_state) that returns the cost of transitioning from the current state to the next state via the given action.

By carefully defining these five components, we create a structured representation of the problem that AI algorithms can work with. This formulation allows for the systematic exploration of the state space, enabling AI systems to find optimal or near-optimal solutions to complex problems.

Examples of Problem Formulation

To better understand how these five components work together, let's examine a few classic AI problems and how they can be formulated using this framework.

8-Puzzle Problem

The 8-puzzle is a sliding puzzle that consists of a 3x3 grid with eight numbered tiles and one empty space. The goal is to rearrange the tiles to reach a specific configuration.

1. Initial State: Any valid configuration of the puzzle, e.g.,

2. Actions: Sliding a tile into the empty space (Up, Down, Left, Right).

3. Transition Model: Moving a tile into the empty space creates a new state.

4. Goal Test: Checking if the current state matches the goal configuration cab be:

5. Path Cost: Each move typically has a cost of 1, so the path cost is the number of moves made.

N-Queens Problem

The N-Queens problem involves placing N chess queens on an NxN chessboard so that no two queens threaten each other. Two queens threaten each other if they are in the same row, column, or diagonal. This following illustrates one possible solution to the 8-Queens problem, where eight queens are placed on the chessboard such that no two queens threaten each other.

1. Initial State: An empty NxN chessboard.

2. Actions: Placing a queen in any empty square of the next row.

3. Transition Model: Adding a queen to the board in the chosen position.

4. Goal Test: Checking if N queens are placed on the board without any conflicts.

5. Path Cost: Often not relevant for this problem, as we're more interested in finding a valid solution than optimizing moves.

Maze Solving

Consider a robot navigating through a maze to find an exit. The maze has multiple paths, some leading to dead ends and others to the exit. Here's a visual representation of such a maze:

1. Initial State: The red circle is the robot's starting position in the maze.

2. Actions: Moving in available directions (Up, Down, Left, Right).

3. Transition Model: Updating the robot's position based on the chosen move.

4. Goal Test: Checking if the current position is the maze exit (green square).

5. Path Cost: The number of moves made, or the distance traveled if the maze has weighted paths.

The Power of Abstraction

What's remarkable about this problem formulation approach is its versatility. Despite the apparent differences between sliding puzzles, chess queen placement, and maze navigation, they can all be abstracted and represented using the same five components.

This abstraction allows us to apply the same AI search algorithms (like BFS, DFS, or A*) to solve these diverse problems without changing the core algorithm. The algorithm operates on the abstract representation of states, actions, and goals, not on the specific details of tiles, queens, or maze walls. The algorithm remains the same; only the problem-specific implementations of the five components change. This powerful abstraction is what makes search algorithms in AI so versatile and widely applicable across various domains.

The Solution:

Now that we've formulated our problem, let's explore a general solution approach using a tree search algorithm. This algorithm systematically explores the state space by expanding nodes in a search tree, where each node represents a state in the problem space.

Tree Search Algorithm

The Tree Search algorithm is a systematic approach to exploring the state space of a problem. Here's how it works:

1. Initialize the frontier with the initial state of the problem.
2. Enter a loop that continues until a solution is found or all possibilities are exhausted:

• If the frontier is empty, return failure (no solution exists).
• Remove a state from the frontier for examination.
• If this state is the goal state, return success (solution found).
• If not the goal, expand the state by applying all possible actions.
• Add the resulting new states to the frontier.

Tree-search (problem p) returns path
  frontier = [p.initial]
	loop:
		if frontier is empty: return fail
		state = frontier.pop()
		if p.goaltest(state): return node
		for a in p.action(state):
			frontier.add[p.result(state,a)]

Graph Search Algorithm

Tree search algorithm does not keep track of visited states, which can lead to redundant exploration of states. Graph search algorithm addresses this issue by maintaining a set of visited states and avoiding re-expansion of states that have already been encountered.

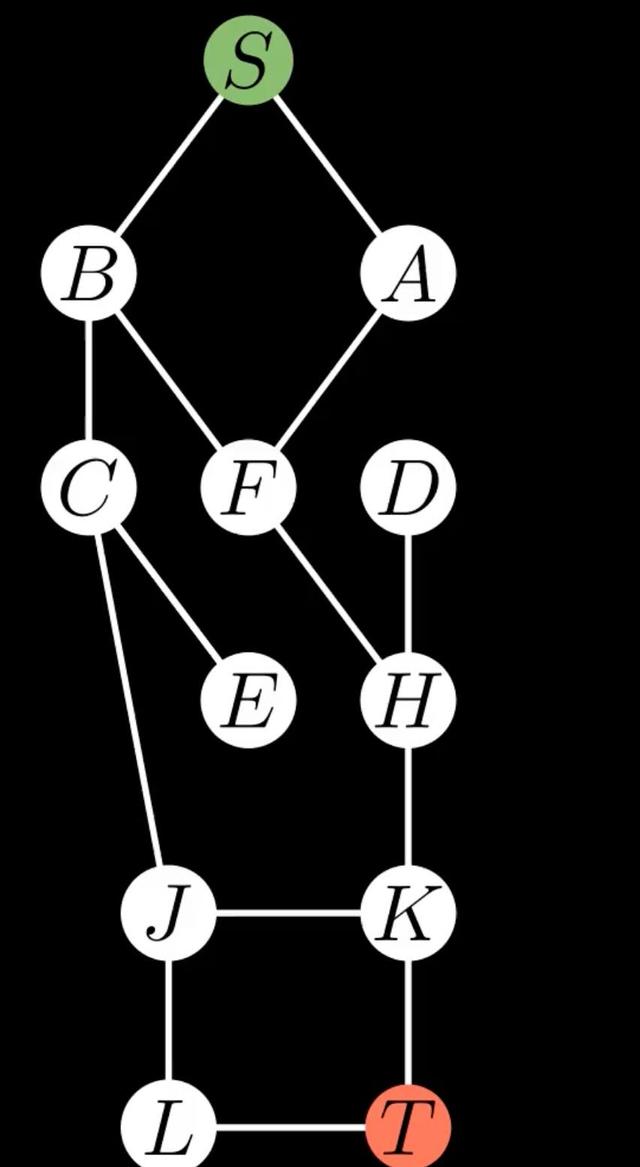
For example, in the figure where S is the start state and T is the goal state, the tree search algorithm might proceed as follows:

1. Start at S and add A and B to the frontier.
2. Explore A, which adds S and F to the frontier.
3. Potentially re-explore S, leading to a cycle.

The Graph Search algorithm improves upon the Tree Search by keeping track of explored states. This enhancement addresses a key limitation of the Tree Search algorithm, i.e Avoids Redundant Exploration. By maintaining a set of explored states, the Graph Search algorithm prevents revisiting states that have already been examined. This is particularly useful in problems where multiple paths can lead to the same state.

The key modification in the Graph Search algorithm is the introduction of an 'explored' set:

Graph-search (problem p) returns path
  frontier = [p.initial]
  explored = set()  // Set to keep track of explored states
  loop:
    if frontier is empty: return fail
    state = frontier.pop()
    if p.goaltest(state): return node
    explored.add(state)  // Add the current state to explored set
    for a in p.action(state):
      child = p.result(state, a)
      if child not in explored and child not in frontier:
        frontier.add(child)

To further illustrate the Graph Search algorithm, let's look at a visual representation:

This video demonstrates how the Graph Search algorithm efficiently explores the state space, avoiding redundant paths and cycles by keeping track of explored states.

Implementing the Graph Search Algorithm

The Node class represents a single state in the search tree, containing information about the state, its parent, and the action taken to reach it.

class Node():
    def __init__(self, state, parent, action):
        self.state = state
        self.parent = parent # parent of the current node
        self.action = action # action that was taken to reach this node

Let formulate the problem of finding a path from the start state to the goal state in a graph.

class GraphProblem():
    
    def __init__(self, vertices, edges, start, goal):
        self.vertices = vertices
        self.edges = edges
        self.start = start
        self.goal = goal
            
    def initial_state(self):
      return self.start

    def goal_test(self, state):
      return state == self.goal
      
    def result(self, state):    
        connected_actions = []
        for edge in self.edges:
            if edge[0] == state:
                connected_actions.append((edge[1], edge[1]))  # (action, resulting state)
            elif edge[1] == state:
                connected_actions.append((edge[0], edge[0]))  # (action, resulting state)
        return connected_actions

The graph_search function implements the Graph Search algorithm, which explores the state space to find a solution to the given problem.

def graph_search(problem):
    # Initialize frontier to just the starting position
    start = Node(state=problem.initial_state(), parent=None, action=None)
    frontier = QueueFrontier(); 
    frontier.add(start)
    
    # Initialize an empty explored set
    explored = set()
    
    # Keep looping until solution found
    while True:
        # If nothing left in frontier, then no path
        if frontier.empty():
            raise Exception("no solution")

        # Choose a node from the frontier
        node = frontier.remove()

        # Mark node as explored
        explored.add(node.state)

        # If node is the goal, then we have a solution
        if problem.goal_test(node.state):
            actions = []
            cells = []
            while node.parent is not None:
                actions.append(node.action)
                cells.append(node.state)
                node = node.parent
            
            actions.append(node.action)
            cells.append(node.state[0])
            
            actions.reverse()
            cells.reverse()
            solution = (actions, cells)
            return solution, explored

        # Add neighbors to frontier
        for action, state in problem.result(node.state):
            if not frontier.contains_state(state) and state not in explored:
                child = Node(state=state, parent=node, action=action)
                frontier.add(child)

Let create the problem instance and call the graph_search function.

vertices = ['S', 'A', 'B', 'C', 'D', 'E', 'F', 'H', 'J', 'K', 'L', 'T']
edges = [
    ('S', 'A'), ('S', 'B'),
    ('A', 'F'),
    ('B', 'F'), ('B', 'C'),
    ('C', 'E'),
    ('D', 'H'),
    ('C', 'J'),
    ('F', 'H'),
    ('H', 'K'),
    ('J', 'L'),
    ('K', 'J'), ('K', 'T'),
    ('L', 'T')
]
problem = GraphProblem(vertices, edges, 'S', 'T')
solution, explored, res = graph_search(problem)

The visualization of the search process is shown above.

Breadth-First Search (BFS) and Depth-First Search (DFS)

One thing to note is that BFS and DFS are special cases of the Graph Search algorithm. It all depends how the frontier is implemented. We have omitted the implementation of the frontier in the above code. If we use a queue as the frontier, we get BFS. If we use a stack as the frontier, we get DFS.

class StackFrontier():
    def __init__(self):
        self.frontier = []
    def add(self, node):
        self.frontier.append(node)
    def contains_state(self, state):
        return any(node.state == state for node in self.frontier)
    def empty(self):
        return len(self.frontier) == 0
    def remove(self):
        if self.empty():
            raise Exception("empty frontier")
        else:
            node = self.frontier.pop()
            return node

class QueueFrontier(StackFrontier):
    def remove(self):
        if self.empty():
            raise Exception("empty frontier")
        else:
            node = self.frontier.pop(0)
            return node

In our implementation of the graph_search algorithm, we employ a stack as the frontier, which allows us to execute Depth-First Search (DFS).

frontier = StackFrontier()

Let's visualize the search process for DFS.

Uniform Cost Search (UCS)

In our previous implementations of graph search algorithms, we have assumed that the cost of traversing each edge is uniform, specifically a cost of 1. This simplification allows us to focus on the structure of the graph and the search process itself. However, in real-world scenarios, the cost of traversing edges can vary significantly based on factors such as distance, time, or resource consumption.

When we need to account for varying path costs, we turn to Uniform Cost Search (UCS). UCS is an extension of the graph search algorithm that prioritizes paths based on their cumulative cost rather than just the number of edges traversed. By using a priority queue as the frontier, UCS ensures that the least costly path is explored first, leading to an optimal solution when costs are taken into account.

To implement UCS, we would modify our frontier to use a priority queue, allowing us to efficiently retrieve the node with the lowest path cost at each step of the search process. This adjustment enables us to handle graphs where edge costs differ, ensuring that our search algorithm remains effective and optimal.

# Priority Queue Frontier
import heapq
class PQueueFrontier(StackFrontier):
    def __init__(self):
        self.frontier = []
    def add(self, node):
        heapq.heappush(self.frontier, node)
    def contains_state(self, state):
        return any(node.state == state for node in self.frontier)
    def empty(self):
        return len(self.frontier) == 0
    def remove(self):
        if self.empty():
            raise Exception("empty frontier")
        else:
            node = heapq.heappop(self.frontier)
            return node

The algorithm is adjusted to use the priority queue frontier. We also need to modify the node class to include the cost of the path from the start node to the current node.

class Node():
  def __init__(self, state, parent, action, cost):
    self.state = state
    self.parent = parent
    self.action = action
    self.cost = cost
  def __lt__(self, other):
    return self.gcost+self.hcost < other.gcost+other.hcost

The updated graph_search function is as follows:

def uniform_cost_search(problem): 
  # Initialize frontier to just the starting position
  start = Node(state=problem.start, parent=None, action=None, gcost=0)
  frontier = PQueueFrontier()
  frontier.add(start)
  # Initialize an empty explored set
  explored = set()
  # Keep looping until solution found
  while True:
      # If nothing left in frontier, then no path
      if frontier.empty():
          raise Exception("no solution")
      # Choose a node from the frontier
      node = frontier.remove()
      # Mark node as explored
      explored.add(node.state)
      # If node is the goal, then we have a solution
      if problem.goal_test(node.state):
        actions = []
        cells = []
        while node.parent is not None:
            actions.append(node.action)
            cells.append(node.state)
            node = node.parent
        actions.reverse()
        cells.reverse()
        solution = (actions, cells)
        return solution, explored
      # Add neighbors to frontier
      for action, state in problem.result(node.state):
        #if not frontier.contains_state(state) and state not in explored:
        if state not in explored:
          child = Node(state=state, parent=node, action=action, gcost=node.gcost+problem.path_cost(node.state, state))
            frontier.add(child)

Let's create the problem instance and call the uniform_cost_search function.

vertices = ['S', 'A', 'B', 'C', 'D', 'E', 'F', 'H', 'J', 'K', 'L', 'T']
edges = [
    ('S', 'A', 2), ('S', 'B', 10),
    ('A', 'F', 4),
    ('B', 'F', 2), ('B', 'C', 5),
    ('C', 'E', 5),
    ('D', 'H', 3),
    ('C', 'J', 12),
    ('F', 'H', 8),
    ('H', 'K', 5),
    ('J', 'L', 4),
    ('K', 'J', 1), ('K', 'T', 7),
    ('L', 'T', 5)
]
problem = GraphProblem(vertices, edges, 'S', 'T')
solution, explored = uniform_cost_search(problem)

The visualization of the search process is shown below.

A* Search

The A* search algorithm is a powerful pathfinding and graph traversal method that is widely used in various applications, including AI and robotics. It improves upon the Uniform Cost Search (UCS) by incorporating a heuristic function that estimates the cost to reach the goal from the current node.

The main problem with UCS is that it only considers the cost incurred from the start node to the current node (gcost). This can lead to inefficient exploration of the state space, as UCS may explore paths that are not optimal in terms of reaching the goal. It does not account for how close a node is to the goal, which can result in longer search times and suboptimal solutions.

A* search addresses this limitation by combining the actual cost (gcost) with the estimated cost (hcost) (also called heuristic) to reach the goal. It uses priority queue to implement the frontier, where the priority is the sum of the gcost and hcost. The rest of the algorithm is the same as the UCS.

Let's assume we have a heuristic function that estimates the cost to reach the goal from the current node. Now for each node, we calculate the sum of the gcost and hcost, and use it as the priority of the node in the priority queue. The node with the lowest sum of gcost and hcost is explored first.

Let's define the heuristic function for the same problem and and visualize the search process.

vertices = ['S', 'A', 'B', 'C', 'D', 'E', 'F', 'H', 'J', 'K', 'L', 'T']
heuristics =[10,  6,   5,   2,   5,   1,  100,  2,   3,   100, 4,   0]

The A* algorithm demonstrates a more efficient exploration of the search space compared to the Uniform Cost Search (UCS) algorithm, as it tends to explore fewer nodes. While the difference in performance may not be substantial for smaller problems, it becomes increasingly significant in larger and more complex scenarios. This efficiency is primarily due to the incorporation of a heuristic function, which guides the search process by estimating the cost to reach the goal from the current node.

However, it is crucial to adhere to certain constraints when designing the heuristic function. Specifically, the heuristic must be admissible, meaning it should never overestimate the actual cost to reach the goal. This property ensures that the A* algorithm remains optimal, as it guarantees that the estimated costs do not lead to suboptimal paths being chosen. Additionally, the heuristic should ideally be consistent, or monotonic, which means that the estimated cost from the current node to the goal should not exceed the cost of reaching a neighboring node plus the cost from that neighbor to the goal. In naviation problem, straight line distance is a good heuristic as it is admissible and consistent.

Characteristics of Search Algorithms

The environment in which the search algorithms discussed above operate is characterized by three key properties: it is fully observable, meaning that all relevant information about the current state is available to the agent; deterministic, indicating that the outcome of any action taken by the agent is predictable and consistent; and static, which implies that the environment does not change while the agent is deliberating or executing its actions.

Conclusion

In conclusion, search algorithms such as Breadth-First Search (BFS), Depth-First Search (DFS), Uniform Cost Search (UCS), and A* Search all utilize a common strategy of systematically exploring the state space to find solutions to complex problems. The primary difference among these algorithms lies in how they implement the frontier. BFS uses a queue to explore nodes level by level, while DFS employs a stack to explore as far down a branch as possible before backtracking. UCS prioritizes nodes based on the lowest path cost, and A* Search combines this with a heuristic to estimate the cost to the goal. Understanding the formulation of problems, including the initial state, actions, transition model, goal test, and path cost, is essential for effectively applying these algorithms.

FAQs

1. What is a search problem in AI?

In AI problem-solving, a search problem involves finding an efficient solution within a complex environment. Imagine navigating from one point to another; the search problem would be to determine the optimal route.

2. What is a state space?

The state space represents all possible situations or configurations that can occur in a problem. In navigation, each state might represent a different location or intersection. AI problem-solving often involves an offline exploration of this state space, where the system examines various possibilities without actually moving in the real world.

3. How do search algorithms work?

Search algorithms systematically traverse the state space, evaluating different paths and outcomes to find the best solution. They achieve this by:

• Defining the initial state (starting point)
• Identifying possible actions (moves or decisions) from each state
• Determining the transition model (how actions change the state)
• Implementing a goal test (checking if a state is the goal)
• Assigning path costs (numeric costs to evaluate efficiency)

By carefully defining these components, AI systems can explore the state space systematically and find optimal solutions.

4. What is a tree search algorithm?

This algorithm systematically explores the state space by expanding nodes in a search tree. Each node represents a state in the problem. The algorithm follows these steps:

1. Initialize with the initial state.
2. Enter a loop that continues until a solution is found or all possibilities are exhausted.
   • If the frontier (states to explore) is empty, it returns failure.
   • A state is removed from the frontier for examination.
   • If this state is the goal, it returns success.
   • If not the goal, it expands the state by applying all possible actions.
   • The resulting new states are added to the frontier.

5. What is a graph search algorithm?

This algorithm improves upon the tree search algorithm by addressing redundant exploration of states. It maintains a set of visited states and avoids re-expanding them. This is particularly useful in problems where multiple paths can lead to the same state.

6. What are Breadth-First Search (BFS) and Depth-First Search (DFS)?

These are special cases of the graph search algorithm depending on how the frontier is implemented:

• BFS: Uses a queue as the frontier, exploring all possibilities at a given depth before moving to the next depth. This ensures all shallower solutions are found before deeper ones.
• DFS: Uses a stack as the frontier, exploring a single path deeply until a solution is found or a dead end is reached. It then backtracks and explores another path.

7. What is Uniform Cost Search (UCS)?

This algorithm extends graph search to consider varying path costs. It utilizes a priority queue as the frontier, prioritizing paths with the lowest cumulative cost. This ensures the most cost-effective solution is found when edge costs differ.