Solving Constraint Satisfaction Problems in AI: Backtracking, Arc Consistency, and Heuristics

Introduction

In this blog post, we will explore Constraint Satisfaction Problems (CSPs), which are a class of computational problems that involve finding values for a set of variables that satisfy a given set of constraints. We will discuss the formal definition of CSPs, the concept of constraint propagation, and various algorithms used to solve CSPs, such as backtracking search and arc consistency.

CSP is formally defined by:

• A finite set of variables $X_i$
• A domain $D_i$ from which each variable $X_i$ takes its values
• A finite set of constraints $C_j$, which restrict the values that variables can take

A state in CSP is an assignment of values from the domain to variables, while a Goal state (or a consistent assignment) is a complete assignment of values that does not violate any constraints.

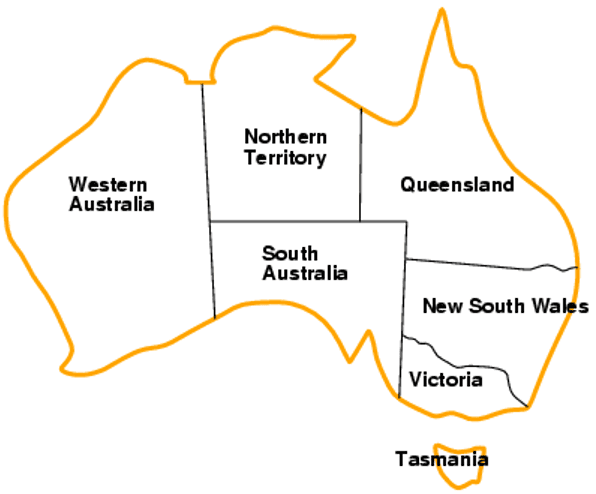
Lets say we want to color the map of Australia using colors {Red, Blue and Green} and the restrition is that neighbouring states can not have the same color. The variables in this problem are the states of Australia, and the domain is the set of colors {Red, Blue, Green}. The constraints are that neighboring states cannot have the same color.

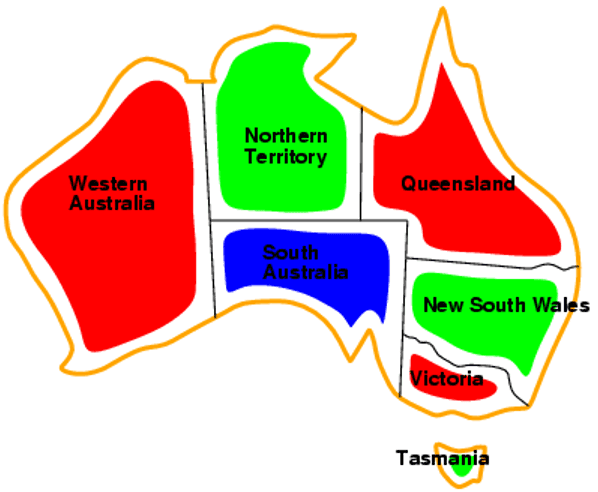
The solution to this CSP is a complete assignment of colors to states that satisfies all the constraints such as the one shown on the right.

Varieties of constraints

There are different types of constraints that can be used in CSPs, such as:

• Unary constraints: Constraints involving a single variable, such as $X_i \neq Red$.
• Binary constraints: Constraints involving pairs of variables, such as $X_i \neq X_j$.
• Higher-order constraints: Constraints involving more than two variables, such as $X_i + X_j + X_k \leq 10$.
• Global constraints: Constraints that involve an arbitrary number of variables, such as AllDifferent, which requires that all variables take distinct values.

Constrain Graph

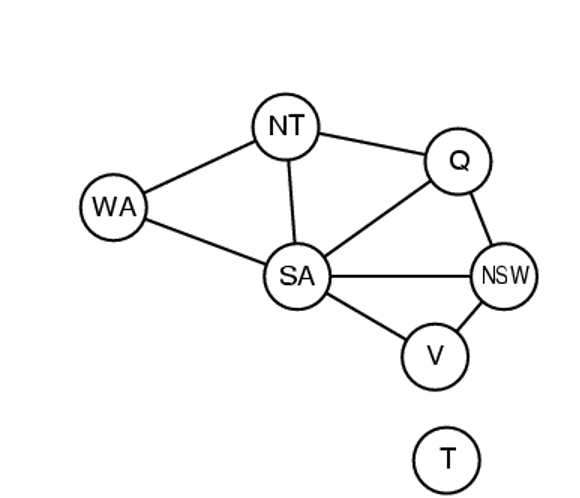
A constraint graph is a graphical representation used to model Constraint Satisfaction Problems. It consists of nodes representing variables and edges representing constraints between variables. The constraint graph provides a visual representation of the relationships between variables and constraints in a CSP. It is mostly used with Binary Constraints.

CSP Algorithms

A CSP can easily be expressed as a standard search problem with the following components:

• state: a set of variables each of which has been assignments a value from the domain (factored representation of the state)
• initial state: the empty assignment
• Result function: assigns a value to an unassigned variable that does not violate any constraints
• goal test: the current assignment is complete and satisfies all constraints

Backtracking Search

Given that we are assigning a value to one variable at a time, every solution would appear at depth $n$ with $n$ variables. This implies use Depth First Search to explore the state space. The algorithm is as follows:

1. Choose a variable to assign a value to.
2. Choose a value from the domain of the variable.
3. Assign the value to the variable.
4. Check if the assignment violates any constraints.
5. If the assignment is consistent, move to the next variable.
6. If the assignment is inconsistent, backtrack and try a different value for the variable.

Example - Crossword Puzzle

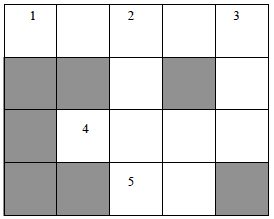
Consider a crossword puzzle where we need to fill in words that satisfy both the horizontal and vertical constraints. The variables are the words to be filled in {X1, X2, X3, X4, X5}, and the domain is the set of possible words that can fit in the puzzle. The constraints are that the words must satisfy both the horizontal and vertical words they intersect with.

Variables: X1, X2, X3, X4, X5. The position of the variables in the puzzle is labeled 1,2,3,4,5

Domain values:

• X1 can be assigned {hoses, laser, sheet, snail, steer}
• X2 can be assigned {hike, aron, keet, earn, same}
• X3 can be assigned {run, sun, let}
• X4 can be assigned {hike, aron, keet}
• X5 can be assigned {no, be}

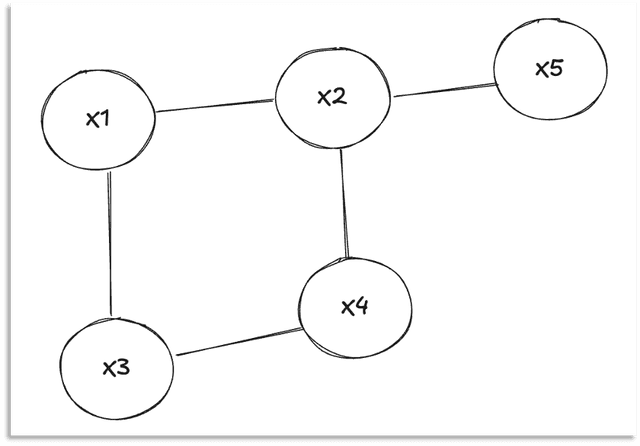
All constraints are binary. The constraint graph is shown on the right.

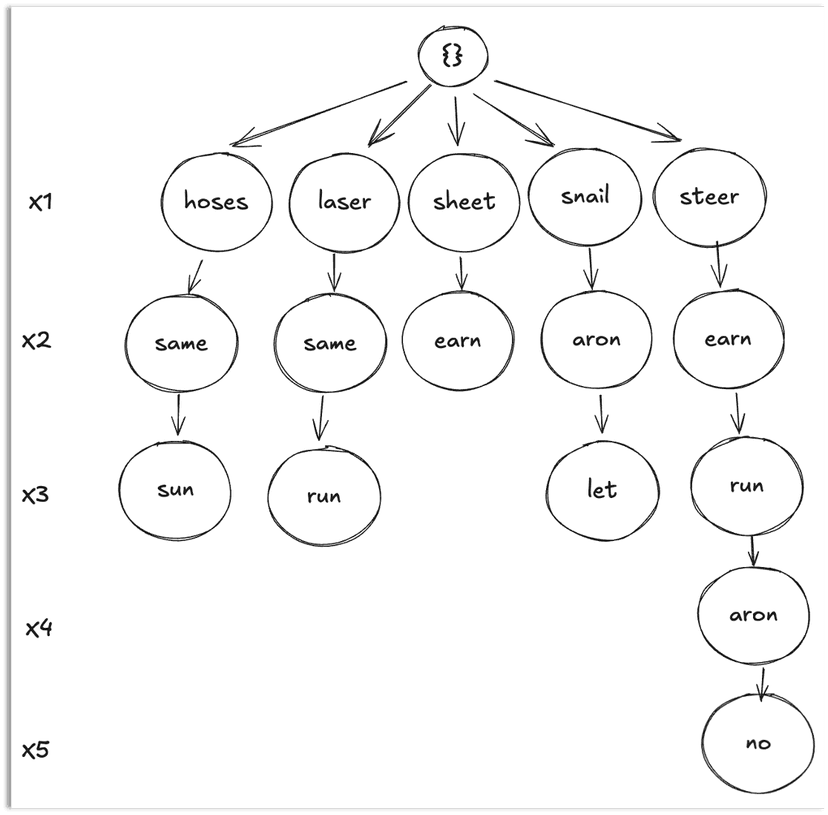
The backtracking search algorithm can be used to solve this crossword puzzle by assigning values to variables one at a time and backtracking when a constraint is violated. The search tree is shown below where at each level one variable is assigned a value. IF there are no legal values left for a variable, the search backtracks to the other branch.

Improving Backtracking Search Efficiency

The basic backtracking search can be enhanced by using heuristics to guide variable selection at each step. In the solution we discussed earlier, we assigned values sequentially, starting with (X_1), then (X_2), and so on. However, by applying heuristics, we can choose the variable that is most likely to lead to a solution with fewer backtracks. Some useful heuristics include:

Minmum Remaining Values (MRV)

MRV is a heuristic used to select the variable that has the fewest legal values left in its domain. This heuristic is used to reduce the branching factor of the search tree.

Forward Checking

Forward checking is a technique used to reduce the search space by eliminating values from the domain of unassigned variables that are inconsistent with the current assignment. It is done by checking the constraints between the current variable and the unassigned variables.

Lets apply the above backtracking search along with the above two techniques to the crossword puzzle example. The search will start with the variable with the fewest legal values left in its domain and eliminate values from the domain of unassigned variables that are inconsistent with the current assignment. So we started with X5 as it has the fewest legal values in the domain. Then the values from the domain of X2 are eliminated as they are inconsistent with the assignment of X5 and so on. The search tree is shown below.

Degree heuristic

When there are multiple variables with the same number of legal values left in their domain, the Degree heuristic is used. This heuristic selects the variable that is involved in the most constraints with the remaining variables. For example, in the crossword puzzle, Degree heuristic would choose X2, as it has the highest degree in the constraint graph. Similarly, in the map coloring problem, the node with the largest degree, SA, will be selected.

Arc Consistency

Arc consistency is a technique used to reduce the search space by ensuring local consistency between variables. It involves identifying all the constraints between pairs of variables $(X_i \rightarrow X_j)$ and then making each arc consistent. An arc $X_i \rightarrow X_j$ is considered consistent if, for every value of $X_i$, there exists at least one allowed value for $X_j$ that satisfies the constraint. If the arc is not consistent, remove values from the domain of $X_i$ so that the remaining values are consistent with the values of $X_j$. It is applied in CSP involving binary constraints.

The most popular algorithm for applying arc-consistency is called AC-3 algorithm which is as follows:

Algorithm AC-3(CSP):
  Initialize a queue Q with all arcs (Xi, Xj) where Xi and Xj are neighbors
  While Q is not empty:
    Remove an arc (Xi, Xj) from Q
    If REVISE(CSP, Xi, Xj) is True:
      If the domain of Xi is empty:
        Return False  // CSP is inconsistent
      For each neighbor Xk of Xi (excluding Xj):
        Add (Xk, Xi) to the queue Q
  Return True  // CSP is arc consistent


Procedure REVISE(CSP, Xi, Xj):
  Set Revised = False
  For each value x in the domain of Xi:
    If no value y in the domain of Xj satisfies the constraint between Xi and Xj:
      Remove x from the domain of Xi
      Set Revised = True
  Return Revised

AC-3 starts by initializing a queue with all arcs (pairs of neighboring variables that have constrains) from the CSP. The algorithm then processes each arc in the queue, checking if the domain of the first variable (Xi) can be reduced by removing values that no longer satisfy the constraints with the second variable (Xj). This check is done by the REVISE procedure, which iterates over the values in Xi’s domain and eliminates those that cannot be paired with any valid value in Xj’s domain. If the domain of Xi becomes empty after this revision, the CSP is deemed inconsistent, and the algorithm returns False. If any values are removed from Xi’s domain, the algorithm adds all of Xi’s other neighbors (except Xj) back into the queue for further checks. The algorithm continues until the queue is empty, and if no inconsistencies are found, it returns True, indicating that the CSP is arc-consistent. This approach efficiently propagates the constraints throughout the CSP by reducing domains based on their interdependencies.

If after the application of AC-3, the domain of any variable becomes empty, the CSP is inconsistent and has no solution. If all variables have a single value in their domain, the CSP is consistent but this does not guarantee a unique solution.

If there are more than one value in the domain of each variable, the CSP is arc consistent but may have multiple solutions or no solution at all. Backtracking search can be used to find a solution in this case.

**Reference: **

• Russell, Stuart J., and Peter Norvig. Artificial Intelligence: A Modern Approach. Pearson, 2021.

Conclusion

The constraint satisfaction problem is a powerful framework for modeling and solving problems that involve finding values for a set of variables that satisfy a given set of constraints. We discussed the formal definition of CSPs, the concept of constraint propagation, and various algorithms used to solve CSPs, such as backtracking search and arc consistency. By applying these algorithms, we can efficiently search the state space and find solutions to complex problems that involve constraints between variables. CSPs have applications in various domains, such as scheduling, planning, and optimization, making them a valuable tool in artificial intelligence and computer science.

FAQs

What is a Constraint Satisfaction Problem (CSP)? A Constraint Satisfaction Problem (CSP) involves finding values for a set of variables that satisfy a given set of constraints. Each variable is assigned a value from a specified domain, and the goal is to find an assignment that doesn’t violate any constraints. CSPs are used in various applications, such as scheduling, map coloring, and puzzle solving.

How are CSPs defined? A CSP is defined by:

• A finite set of variables.
• A domain for each variable, which specifies the possible values that the variable can take.
• A set of constraints that restrict how the variables can interact or be assigned values.

What are the different types of constraints in CSPs? The main types of constraints include:

• Unary constraints: Involve a single variable, such as $X_i \neq Red$.
• Binary constraints: Involve pairs of variables, such as $X_i \neq X_j$.
• Global constraints: Involve arbitrary numbers of variables, like ensuring all variables have distinct values.

What is a constraint graph? A constraint graph is a graphical representation of a CSP where each node represents a variable, and each edge represents a constraint between two variables. It visually illustrates how variables are related and constrained in a CSP, often used for binary constraints.

What algorithms are used to solve CSPs? Common algorithms used to solve CSPs include:

• Backtracking search: A depth-first search method where variables are assigned values one at a time, and the search backtracks if a constraint is violated.
• Arc consistency: An optimization technique that ensures local consistency by checking that for every value of a variable, there is a corresponding valid value in neighboring variables' domains.

How does backtracking search work in CSPs? Backtracking search assigns values to variables one by one, checking for constraint violations. If an assignment is inconsistent with the constraints, the algorithm backtracks to try different values for the variables. This process continues until all variables are assigned valid values or it is determined that no solution exists.

What is the role of heuristics in improving backtracking search? Heuristics like Minimum Remaining Values (MRV), Forward Checking, and Degree heuristic can help improve the efficiency of backtracking search. MRV selects the variable with the fewest legal values remaining, Forward Checking eliminates inconsistent values from unassigned variables' domains, and the Degree heuristic selects the variable involved in the most constraints to minimize the search space.

What is Arc Consistency, and how does it help in CSPs? Arc consistency is a technique that ensures each variable’s domain is consistent with its neighboring variables. By iterating through the constraints and removing values that do not have valid counterparts in neighboring domains, arc consistency reduces the search space and helps in solving CSPs more efficiently.

How does the AC-3 algorithm work? The AC-3 algorithm ensures arc consistency by iterating through a queue of arcs, where each arc represents a constraint between two variables. If a variable's domain is reduced due to inconsistency with another variable, the affected variable's neighbors are added back to the queue for further checking. The algorithm continues until all arcs are consistent or a contradiction is found.

Can CSPs have multiple solutions? Yes, a CSP can have multiple solutions.

What are some practical applications of CSPs? CSPs are used in various domains, including:

• Scheduling: Assigning tasks to time slots without conflicts.
• Map coloring: Coloring maps such that neighboring regions don’t share the same color.
• Puzzle solving: Solving problems like Sudoku or crossword puzzles, where each variable (e.g., a cell or a word) has specific constraints.