From Edges to Corners: Exploring Harris Corner Detection in Computer Vision

Introduction

As humans, when we observe images, we instinctively identify distinctive keypoints or salient features. We then leverage the surrounding context to recognize and understand the relationships between these keypoints. Similarly, computer vision algorithms adopt a parallel approach. They begin by detecting keypoints in an image, identifying key structures or points of interest. Subsequently, these algorithms proceed to match these keypoints by analyzing the contextual information surrounding them. This methodology aligns with how humans naturally perceive and interpret visual information, contributing to the effectiveness of computer vision in tasks such as object recognition and image matching

Image Alignment

Consider an application where accurately identifying key points within an image is crucial. Given two images depicting the same object, how can we effectively combine their information? This can be achieved through a three-step process:

Image Source: Darya Frolova, Denis Simakov

Characteristics of good keypoints

Accurate keypoint detection is crucial for various applications, but what makes a keypoint effective? Let's examine the key characteristics that define a suitable keypoint:

• Sky (a): The sky is not an ideal keypoint due to its minimal variation and high likelihood of matching similar sky areas elsewhere in the image.

• Edges (b): Edges show variation in a specific direction and may match other patches along the same edge, making them somewhat directional but less distinctive.

• Corners (c): Corners are the most promising keypoints, as they exhibit unique, distinctive features that set them apart from surrounding areas, making them stronger candidates for reliable keypoint detection.

Corners exhibit several key attributes that make them ideal keypoints:

• Compactness and Efficiency: They represent a fraction of the total image pixels, ensuring efficient processing.
• Saliency: Corners are highly distinctive, standing out clearly from their surroundings.
• Locality: They occupy a small, localized area, which enhances their robustness to clutter and occlusion.
• Repeatability: Corners can be reliably detected across different images, even under various geometric and photometric changes.

Applications

Keypoints are essential for various applications, including:

• Image Alignment: Ensuring that images from different sources or viewpoints match up accurately.
• 3D Reconstruction: Building three-dimensional models from two-dimensional images.
• Motion Tracking: Monitoring and analyzing the movement of objects within a sequence of images.
• Robot Navigation: Guiding robots through environments by recognizing and interpreting visual features.
• Database Indexing and Retrieval: Efficiently organizing and retrieving images based on their content.

To detect corners in images, we can use algorithms like the Harris corner detector, which is specifically designed to identify corner points effectively.

Harris Corner Detector

The Harris Corner Detector is a popular algorithm for detecting corners in images. It works by analyzing the gradients within a window. The gradient computation is computed using convolution. Imagine three rectangular regions within an image where we want to analyze if a corner exists or not. These three regions are shown as red, blue and green rectangles.

For each region, we compute the derivatives $\partial x$ and $\partial y$ and analyze gradient distribution:

• Red Rectangle: Both $\partial x$ and $\partial y$ are near zero, indicating a flat region.
• Green Rectangle: $\partial x$ shows variation while $\partial y$ remains near zero, indicating an edge.
• Blue Rectangle: Both $\partial x$ and $\partial y$ show variation, indicating a corner.

Let's plot the $\partial x$ and $\partial y$ values for the three rectangular regions. The distribution of these values will help us determine whether these regions are corners or not.

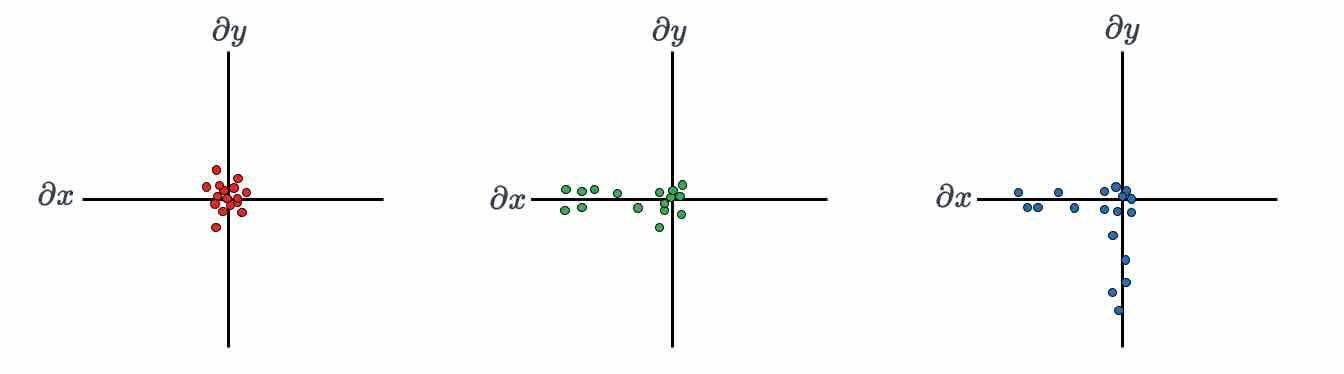
Now we ca can fit an ellipse and analyze its axes. In corners, both the major ($\lambda_1$) and minor axes ($\lambda_2$) of the ellipse are large.

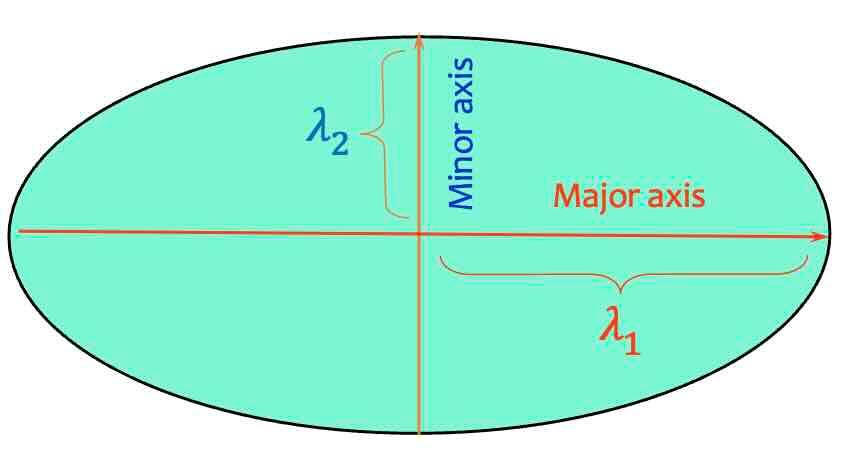
• $\lambda_1$ and $\lambda_2$ both small: No significant gradient, flat region
• $\lambda_1$ >> $\lambda_2$: Gradient in one direction, indicating an edge.
• $\lambda_1$ and $\lambda_2$ similar: Multiple gradient directions, indicating a corner.

The eigenvalues $\lambda_1$ and $\lambda_2$ can be obtained from the Harris matrix $H$, which is computed as:

$$H = \begin{bmatrix} \sum_i w_i I_x^2 & \sum_i w_i I_x I_y \\ \sum_i w_i I_x I_y & \sum_i w_i I_y^2 \end{bmatrix}$$

where $I_x$ is the image gradient w.r.t $x$ and where $I_y$ is the image gradient w.r.t $y$. Essentially Harris matrix $H$ captures the gradient changes in both the $x$ and $y$ directions within a local window. The eigenvalues $\lambda_1$, $\lambda_2$ of this matrix tell us about the variation of gradient distribution in different directions. Here's an improved and more polished version of your text:

The Determinant of H is given by:

$$\text{det}(H) = \lambda_1 \lambda_2$$

The Trace of H is:

$$\text{trace}(H) = \lambda_1 + \lambda_2$$

The Corner Response (R) is calculated as:

$$R = \text{det}(H) - k \times (\text{trace}(H))^2 = \lambda_1 \lambda_2 - k \times (\lambda_1 + \lambda_2)^2$$

A higher value of $R$ indicates a more distinct and prominent corner. The parameter $k$ allows us to balance between precision and recall. A higher $k$ reduces false positives, leading to high precision, but may miss true corners. Conversely, a lower $k$ detects more corners, enhancing recall, but may increase false positives."

The Algorithm

To implement the Harris Corner Detector, follow these steps:

1. Compute Partial Derivatives
   Calculate the partial derivatives $I_x$ and $I_y$ at each pixel.

2. Calculate Three Measures
   Compute the following measures: $I_x^2$, $I_y^2$, $I_x I_y$

3. Estimate the Response
   Estimate the corner response $R$ using the formula with-in window region:

   $$R = \text{det}(H) - k \cdot \text{trace}(H)^2$$

   where $H$ is the Harris matrix, $\text{det}(H)$ is the determinant, $\text{trace}(H)$ is the trace, and $k$ is a sensitivity factor.

4. Threshold the Response
   Apply a threshold to the response $R$ to filter out weak responses.

5. Find Local Maxima of Response Function
   Perform Non-Maximum Suppression (NMS) to identify the local maxima in the response function. This helps in pinpointing the corner points.

# OpenCV implementation
# Read the image
image = cv2.imread('<path to image file>', cv2.IMREAD_GRAYSCALE)
# Apply the Harris Corner Detector
harris_response = cv2.cornerHarris(image, blockSize=9, ksize=5, k=0.05)
# Threshold the response to identify corners
threshold = 0.05 * harris_response.max()
corner_mask = (harris_response > threshold).astype(np.uint8) * 255

# Get the x, y coordinates of the corners
#coordinates = np.column_stack(np.where(corner_mask > 0))
coordinates = np.where(corner_mask > 0)
# Display the original image and detected corners
plt.figure(figsize=(10, 10))
plt.subplot(111), plt.imshow(image, cmap='gray')
plt.scatter(coordinates[1], coordinates[0], color='red', marker='.', s=1)
plt.xticks([]), plt.yticks([])

Effect of parameter $k$ on corner detection using Harris Corner detector.

Slider control: k=[0.01, 0.05, 0.2] ( Image Source )

---

Invariance properties of corners

In image matching, the goal is often to find corresponding points or features between two or more images. For this task to be effective, it's essential that the same corner features can be reliably identified across different images, even when those images undergo geometric and photometric transformations.

Image Source: Flickr

Photometric transformations

Photometric transformations refer to operations that alter the intensity or color characteristics of an image without changing its geometric properties. These transformations are applied on a per-pixel basis

• Invariant to Additive Changes in Intensity (Brightness):

  • The Harris Corner Detector remains unaffected by changes in the overall brightness of an image. This means if you uniformly increase or decrease the brightness across the entire image, the Harris Corner Detector will still identify the same corner points. This property is called additive invariance.
  • For example, if you add a constant value to every pixel in the image (making it brighter or darker), the Harris corner response will remain the same, ensuring consistent corner detection regardless of such changes.

• Not Invariant to Scaling of Intensity (Contrast):

  • The Harris Corner Detector is sensitive to changes in contrast. This means if you increase or decrease the contrast of the image (which involves scaling pixel values), the detector might produce different results, identifying different corner points.
  • For example, if the intensity values of the image are multiplied by a factor, the relative differences between pixel values are altered, which can affect the gradient calculations and the resulting corner detection. This lack of invariance to contrast scaling can cause the detector to miss some corners or detect new ones, depending on how the contrast is changed.

In summary, while the Harris Corner Detector is robust to uniform changes in brightness, it can be influenced by changes in contrast, which may affect the accuracy of corner detection.

Geometric transformations

Geometric transformations are operations that change the spatial relationship of points in an image. These transformations include translation, rotation and scaling.

• Translation Invariance:

  • The Harris Corner Detector is invariant to translation. This means if the image is shifted, the corners detected will remain the same, just moved to the new location.

• Rotation Invariance:

  • The Harris Corner Detector is partially invariant to rotation. It can detect the same corners after rotation, but the strength of the detected corners might vary slightly depending on the rotation angle.

• Scaling Invariance:

  • The Harris Corner Detector is not invariant to scaling. When the image is scaled, the detected corners might change because the gradients and pixel values are affected by the scaling operation. This can lead to different corner detection results.

Summary

This blog explores the essentials of the Harris Corner Detector, a crucial tool in computer vision for detecting and analyzing key points within images. It underscores the significance of keypoint detection in various applications, highlighting how identifying distinct features like corners is more effective than focusing on edges or flat regions. The blog also examines the invariance properties of the Harris Corner Detector, noting its robustness to additive changes in brightness while acknowledging its sensitivity to contrast changes and geometric transformations such as scaling and rotation.

FAQs

1. What is the Harris Corner Detector? The Harris Corner Detector is an algorithm used in computer vision to identify corner points in an image. It analyzes the gradients within a small window to detect regions where there are significant changes in both horizontal and vertical directions, indicating the presence of a corner.

2. Why are corners important in computer vision? Corners are distinctive and unique points in an image, making them ideal keypoints for tasks such as image alignment, 3D reconstruction, motion tracking, and object recognition. They provide strong features that can be reliably detected and matched across different images.

3. How does the Harris Corner Detector work? The Harris Corner Detector computes image gradients in the x and y directions within a window around each pixel. It then forms a matrix from these gradients and calculates its eigenvalues. The algorithm uses these eigenvalues to determine whether a region is a corner, edge, or flat area by analyzing the variation in gradients.

4. What are the steps to implement the Harris Corner Detector? The steps include:

1. Computing partial derivatives of the image.
2. Calculating gradient measures like $I_x^2$, $I_y^2$, and $I_x I_y$.
3. Estimating the corner response using the Harris matrix.
4. Thresholding the response to identify significant corners.
5. Performing Non-Maximum Suppression (NMS) to find local maxima and determine precise corner locations.

5. What are the characteristics of good keypoints? Good keypoints are:

• Compact: Representing a small fraction of the total image pixels.
• Salient: Distinctive and standing out from their surroundings.
• Local: Occupying a small area, which makes them robust to occlusion and clutter.
• Repeatable: Can be reliably detected across different images under various conditions.

6. Is the Harris Corner Detector invariant to photometric transformations? The Harris Corner Detector is invariant to additive changes in intensity, meaning it can detect the same corners even if the overall brightness of the image changes. However, it is not invariant to scaling of intensity (contrast changes), which can affect the detection results.

7. Is the Harris Corner Detector invariant to geometric transformations? The Harris Corner Detector is invariant to translation and partially invariant to rotation. However, it is not invariant to scaling, meaning the corners detected can change if the image is resized.

8. What are some applications of the Harris Corner Detector? The Harris Corner Detector is used in various applications such as:

• Image alignment
• 3D reconstruction
• Motion tracking
• Robot navigation
• Database indexing and retrieval

9. What role does the parameter 'k' play in the Harris Corner Detector? The parameter 'k' in the Harris Corner Detector controls the sensitivity of corner detection. A higher 'k' reduces false positives but may miss some corners, while a lower 'k' increases the number of detected corners but may include more false positives.

10. How does the Harris Corner Detector handle changes in image brightness? The Harris Corner Detector is designed to handle additive changes in image brightness, meaning it can consistently detect corners even if the image becomes uniformly brighter or darker.

---